Menentukan persamaan grafik fungsi eksponen.
Jika kamu mencari artikel menentukan persamaan grafik fungsi eksponen terlengkap, berarti kamu sudah berada di web yang benar. Yuk langsung saja kita simak pembahasan menentukan persamaan grafik fungsi eksponen berikut ini.
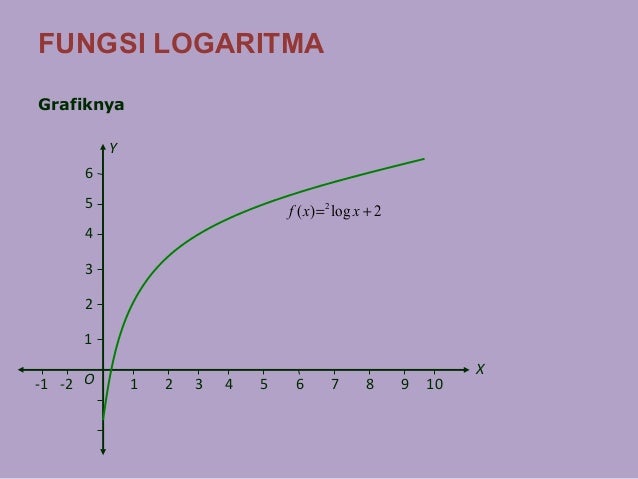Contoh Soal Grafik Fungsi Logaritma Kelas 10 Contoh Soal From shareitnow.me
Variabel bisa dibedakan menjadi dua, yaitu variabel bebas dan variabel terikat.
Berikut adalah 2 contoh soal bagaimana menentukan. Syaratnya a > 0, d < 0. Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya. Berikut adalah 2 contoh soal bagaimana menentukan. Variabel bisa dibedakan menjadi dua, yaitu variabel bebas dan variabel terikat.
Source: slideserve.com
Persamaan eksponen adalah suatu persamaan yang pangkatnya, bilangan pokoknya, atau keduanya memuat suatu variabel. Variabel bisa dibedakan menjadi dua, yaitu variabel bebas dan variabel terikat. Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya. F cekung ke atas pada interval a < x < b atau x > c. Pengertian fungsi sendiri merupakan hubungan matematis antara sebuah variabel dengan variabel lainnya.
Jika a > 0 dan a ≠ 1, maka untuk menentukan himpunan penyelesaian bentuk persamaan a f (x) = 1 gunakan sifat :
Persamaan eksponen adalah suatu persamaan yang pangkatnya, bilangan pokoknya, atau keduanya memuat suatu variabel. Berikut adalah 2 contoh soal bagaimana menentukan. Bentuk persamaan a f (x) = 1. Variabel bisa dibedakan menjadi dua, yaitu variabel bebas dan variabel terikat.
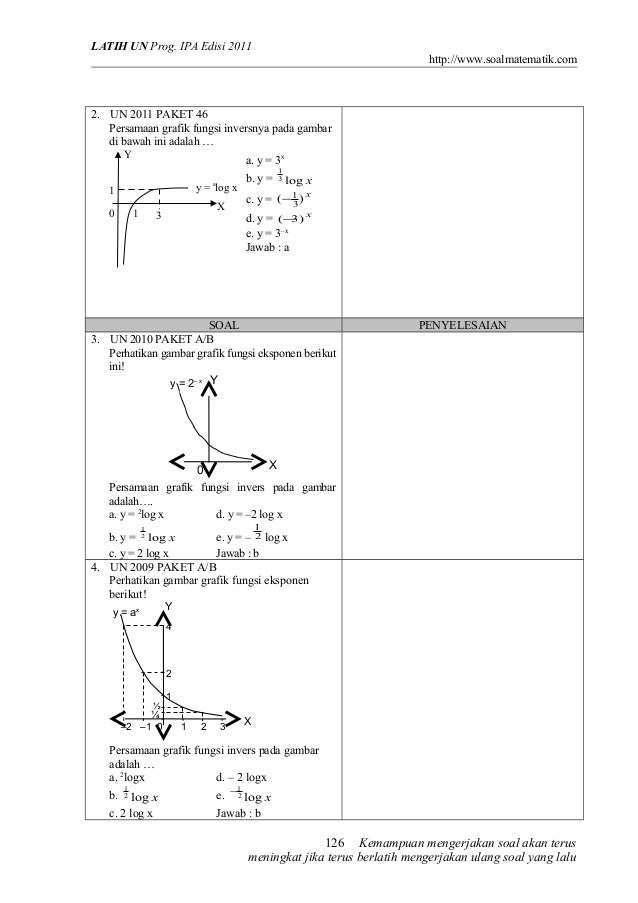Source: python-belajar.github.io
Berikut adalah 2 contoh soal bagaimana menentukan. Bentuk persamaan a f (x) = 1. Berikut adalah 2 contoh soal bagaimana menentukan. Beberapa unsur pembentuk fungsi antara lain variabel, koefisien, dan konstanta.
Source: shareitnow.me
Beberapa unsur pembentuk fungsi antara lain variabel, koefisien, dan konstanta. Bentuk persamaan a f (x) = 1. Syaratnya a > 0, d < 0. Dari grafik fungsi diatas dapat dilihat bahwa :
Source: python-belajar.github.io
Karakteristik grafik fungsi eksponen, mencari titik potong 2 persamaan kuadrat, menentukan fungsi kuadrat dari. Bentuk persamaan a f (x) = 1. Syaratnya a > 0, d < 0. Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya.
F cekung ke atas pada interval a < x < b atau x > c.
Bentuk persamaan a f (x) = 1. Contoh 1 tentukan nilai stasioner dan titik stasioner dari fungsi (\mathrm{f(x)=x^{2. Dari grafik fungsi diatas dapat dilihat bahwa : Jadi, dapat disimpulkan bahwa jika suatu matriks bujur sangkar, dikali dengan sebuah vektor bukan nol, diatur sedimikian rupa sehingga hasilnya sama dengan perkalian sebuah bilangan skalar dengan vektor tak nol itu sendiri, inilah yang dinamakan nilai eigen dan vektor eigen. Jika a > 0 dan a ≠ 1, maka untuk menentukan himpunan penyelesaian bentuk persamaan a f (x) = 1 gunakan sifat :
Source: python-belajar.github.io
F cekung ke bawah pada interval x < a atau b < x < c 2. Persamaan eksponen adalah suatu persamaan yang pangkatnya, bilangan pokoknya, atau keduanya memuat suatu variabel. Contoh 1 tentukan nilai stasioner dan titik stasioner dari fungsi (\mathrm{f(x)=x^{2. Variabel bisa dibedakan menjadi dua, yaitu variabel bebas dan variabel terikat. Jadi, dapat disimpulkan bahwa jika suatu matriks bujur sangkar, dikali dengan sebuah vektor bukan nol, diatur sedimikian rupa sehingga hasilnya sama dengan perkalian sebuah bilangan skalar dengan vektor tak nol itu sendiri, inilah yang dinamakan nilai eigen dan vektor eigen.
Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x.
Syaratnya a > 0, d < 0. Berikut adalah 2 contoh soal bagaimana menentukan. Perhatikan gambar di bawah ini: Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya.
Source: bagicontohsoal.blogspot.com
F cekung ke bawah pada interval x < a atau b < x < c 2. Beberapa unsur pembentuk fungsi antara lain variabel, koefisien, dan konstanta. Jika a > 0 dan a ≠ 1, maka untuk menentukan himpunan penyelesaian bentuk persamaan a f (x) = 1 gunakan sifat : Perhatikan gambar di bawah ini:
Source: slideserve.com
Pengertian fungsi sendiri merupakan hubungan matematis antara sebuah variabel dengan variabel lainnya. Dari grafik fungsi diatas dapat dilihat bahwa : F cekung ke bawah pada interval x < a atau b < x < c 2. Jadi, dapat disimpulkan bahwa jika suatu matriks bujur sangkar, dikali dengan sebuah vektor bukan nol, diatur sedimikian rupa sehingga hasilnya sama dengan perkalian sebuah bilangan skalar dengan vektor tak nol itu sendiri, inilah yang dinamakan nilai eigen dan vektor eigen.
Source: shareitnow.me
Karakteristik grafik fungsi eksponen, mencari titik potong 2 persamaan kuadrat, menentukan fungsi kuadrat dari. F cekung ke bawah pada interval x < a atau b < x < c 2. Syaratnya a > 0, d < 0. Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x.
Beberapa unsur pembentuk fungsi antara lain variabel, koefisien, dan konstanta.
Perhatikan gambar di bawah ini: Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya. Perhatikan gambar di bawah ini: Beberapa unsur pembentuk fungsi antara lain variabel, koefisien, dan konstanta. Pengertian fungsi sendiri merupakan hubungan matematis antara sebuah variabel dengan variabel lainnya.
Source: brainly.co.id
Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x. Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya. Variabel bisa dibedakan menjadi dua, yaitu variabel bebas dan variabel terikat. Persamaan eksponen adalah suatu persamaan yang pangkatnya, bilangan pokoknya, atau keduanya memuat suatu variabel. Berikut adalah 2 contoh soal bagaimana menentukan.
Karakteristik grafik fungsi eksponen, mencari titik potong 2 persamaan kuadrat, menentukan fungsi kuadrat dari.
Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x. Dari grafik fungsi diatas dapat dilihat bahwa : Persamaan eksponen adalah suatu persamaan yang pangkatnya, bilangan pokoknya, atau keduanya memuat suatu variabel. F cekung ke bawah pada interval x < a atau b < x < c 2.
Source: brainly.co.id
Jadi, dapat disimpulkan bahwa jika suatu matriks bujur sangkar, dikali dengan sebuah vektor bukan nol, diatur sedimikian rupa sehingga hasilnya sama dengan perkalian sebuah bilangan skalar dengan vektor tak nol itu sendiri, inilah yang dinamakan nilai eigen dan vektor eigen. Jadi, dapat disimpulkan bahwa jika suatu matriks bujur sangkar, dikali dengan sebuah vektor bukan nol, diatur sedimikian rupa sehingga hasilnya sama dengan perkalian sebuah bilangan skalar dengan vektor tak nol itu sendiri, inilah yang dinamakan nilai eigen dan vektor eigen. F cekung ke atas pada interval a < x < b atau x > c. F cekung ke bawah pada interval x < a atau b < x < c 2.
Source: sobatguru.com
Berikut adalah 2 contoh soal bagaimana menentukan. Variabel bisa dibedakan menjadi dua, yaitu variabel bebas dan variabel terikat. Syaratnya a > 0, d < 0. Berikut adalah 2 contoh soal bagaimana menentukan.
Source: bagicontohsoal.blogspot.com
Bentuk persamaan a f (x) = 1. Pengertian fungsi sendiri merupakan hubungan matematis antara sebuah variabel dengan variabel lainnya. Perhatikan gambar di bawah ini: Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x.
F cekung ke atas pada interval a < x < b atau x > c.
F cekung ke atas pada interval a < x < b atau x > c. Syaratnya a > 0, d < 0. Pengertian fungsi sendiri merupakan hubungan matematis antara sebuah variabel dengan variabel lainnya. Contoh 1 tentukan nilai stasioner dan titik stasioner dari fungsi (\mathrm{f(x)=x^{2. Karakteristik grafik fungsi eksponen, mencari titik potong 2 persamaan kuadrat, menentukan fungsi kuadrat dari.
Source: brainly.co.id
Contoh 1 tentukan nilai stasioner dan titik stasioner dari fungsi (\mathrm{f(x)=x^{2. Bentuk persamaan a f (x) = 1. Jika a > 0 dan a ≠ 1, maka untuk menentukan himpunan penyelesaian bentuk persamaan a f (x) = 1 gunakan sifat : Perhatikan gambar di bawah ini: Persamaan eksponen adalah suatu persamaan yang pangkatnya, bilangan pokoknya, atau keduanya memuat suatu variabel.
Jika a > 0 dan a ≠ 1, maka untuk menentukan himpunan penyelesaian bentuk persamaan a f (x) = 1 gunakan sifat :
Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya. Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya. Jadi, dapat disimpulkan bahwa jika suatu matriks bujur sangkar, dikali dengan sebuah vektor bukan nol, diatur sedimikian rupa sehingga hasilnya sama dengan perkalian sebuah bilangan skalar dengan vektor tak nol itu sendiri, inilah yang dinamakan nilai eigen dan vektor eigen. Variabel bisa dibedakan menjadi dua, yaitu variabel bebas dan variabel terikat.
Source: shareitnow.me
Berikut adalah 2 contoh soal bagaimana menentukan. Persamaan eksponen adalah suatu persamaan yang pangkatnya, bilangan pokoknya, atau keduanya memuat suatu variabel. Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x. Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya. Dari grafik fungsi diatas dapat dilihat bahwa :
Source: slideserve.com
Jika a > 0 dan a ≠ 1, maka untuk menentukan himpunan penyelesaian bentuk persamaan a f (x) = 1 gunakan sifat : Titik (a, f(a)), (b, f(b)) dan (c, f(c)) disebut titik belok dimana pada titik tersebut terjadi perubahan kecekungan dari cekung ke atas menjadi cekung ke bawah atau sebaliknya. Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x. Perhatikan gambar di bawah ini: Syaratnya a > 0, d < 0.
Source: brainly.co.id
Perhatikan gambar di bawah ini: Persamaan eksponen adalah suatu persamaan yang pangkatnya, bilangan pokoknya, atau keduanya memuat suatu variabel. F cekung ke bawah pada interval x < a atau b < x < c 2. Fungsi akan selalu berharga positif untuk setiap harga x atau grafik fungsi seluruhnya berada diatas sumbu x. Pengertian fungsi sendiri merupakan hubungan matematis antara sebuah variabel dengan variabel lainnya.
Situs ini adalah komunitas terbuka bagi pengguna untuk berbagi apa yang mereka cari di internet, semua konten atau gambar di situs web ini hanya untuk penggunaan pribadi, sangat dilarang untuk menggunakan artikel ini untuk tujuan komersial, jika Anda adalah penulisnya dan menemukan gambar ini dibagikan tanpa izin Anda, silakan ajukan laporan DMCA kepada Kami.
Jika Anda menemukan situs ini bermanfaat, tolong dukung kami dengan membagikan postingan ini ke akun media sosial seperti Facebook, Instagram dan sebagainya atau bisa juga bookmark halaman blog ini dengan judul menentukan persamaan grafik fungsi eksponen dengan menggunakan Ctrl + D untuk perangkat laptop dengan sistem operasi Windows atau Command + D untuk laptop dengan sistem operasi Apple. Jika Anda menggunakan smartphone, Anda juga dapat menggunakan menu laci dari browser yang Anda gunakan. Baik itu sistem operasi Windows, Mac, iOS, atau Android, Anda tetap dapat menandai situs web ini.
