Contoh soal relasi antisimetris.
Jika kamu mencari artikel contoh soal relasi antisimetris terlengkap, berarti kamu telah berada di web yang benar. Yuk langsung saja kita simak pembahasan contoh soal relasi antisimetris berikut ini.
06 momen inersia 3 From slideshare.net
Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif.
Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Diberikan himpunan c = {2, 4, 5}. Didefinisikan relasi pada himpunan p dengan r={(1,1. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Pengertian relasi dan fungsi serta perbedaanya.
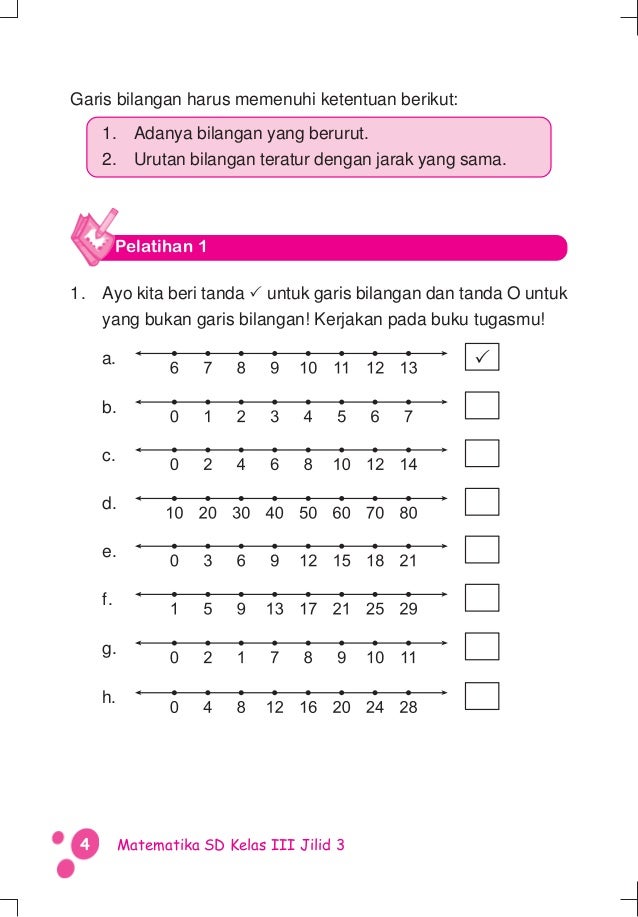Source: slideshare.net
Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Pengertian relasi dan fungsi serta perbedaanya. Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif. Relasi r tersebut bersifat antisimetris.
Didefinisikan relasi pada himpunan p dengan r={(1,1.
Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p. Relasi r tersebut bersifat antisimetris. Pengertian relasi dan fungsi serta perbedaanya. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}.
Source: slideshare.net
Diberikan himpunan c = {2, 4, 5}. Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p. Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif. Relasi r tersebut bersifat antisimetris.
Source: slideshare.net
Misalkan r sebuah relasi pada sebuah himpunan p. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}. Relasi r tersebut bersifat antisimetris. Misalkan r sebuah relasi pada sebuah himpunan p.
Source: youtube.com
Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif. Relasi r tersebut bersifat antisimetris. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke.
Misalkan r sebuah relasi pada sebuah himpunan p.
Didefinisikan relasi pada himpunan p dengan r={(1,1. Relasi r dikatakan bersifat antisimetris, apabila untuk setiap (x,y) ∈ r dan (y,x) ∈ r berlaku x = y. Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}.
Source: youtube.com
Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p. Misalkan r sebuah relasi pada sebuah himpunan p. Pengertian relasi dan fungsi serta perbedaanya. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Relasi r tersebut bersifat antisimetris.
Relasi r tersebut bersifat antisimetris.
Didefinisikan relasi pada himpunan p dengan r={(1,1. Diberikan himpunan c = {2, 4, 5}. Didefinisikan relasi pada himpunan p dengan r={(1,1. Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif.
Source: kanaljabar.com
Didefinisikan relasi pada himpunan p dengan r={(1,1. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p.
Source: youtube.com
Didefinisikan relasi pada himpunan p dengan r={(1,1. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}. Didefinisikan relasi pada himpunan p dengan r={(1,1.
Source: slideshare.net
Relasi r tersebut bersifat antisimetris. Didefinisikan relasi pada himpunan p dengan r={(1,1. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}.
Pengertian relasi dan fungsi serta perbedaanya.
Relasi r tersebut bersifat antisimetris. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Misalkan r sebuah relasi pada sebuah himpunan p. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Diberikan himpunan c = {2, 4, 5}.
Source: slideshare.net
Didefinisikan relasi pada himpunan p dengan r={(1,1. Relasi r tersebut bersifat antisimetris. Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif. Didefinisikan relasi pada himpunan p dengan r={(1,1. Diberikan himpunan c = {2, 4, 5}.
Didefinisikan relasi pada himpunan p dengan r={(1,1.
Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Diberikan himpunan c = {2, 4, 5}. Didefinisikan relasi pada himpunan p dengan r={(1,1.
Source: youtube.com
Relasi r dikatakan bersifat antisimetris, apabila untuk setiap (x,y) ∈ r dan (y,x) ∈ r berlaku x = y. Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}.
Source: slideshare.net
Relasi r dikatakan bersifat antisimetris, apabila untuk setiap (x,y) ∈ r dan (y,x) ∈ r berlaku x = y. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Pengertian relasi dan fungsi serta perbedaanya. Relasi r tersebut bersifat antisimetris.
Source: kanaljabar.com
Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif. Relasi r dikatakan bersifat antisimetris, apabila untuk setiap (x,y) ∈ r dan (y,x) ∈ r berlaku x = y. Didefinisikan relasi pada himpunan p dengan r={(1,1. Relasi r tersebut bersifat antisimetris.
Didefinisikan relasi pada himpunan p dengan r={(1,1.
Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif. Diberikan himpunan c = {2, 4, 5}. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}. Relasi r tersebut bersifat antisimetris. Relasi r disebut relasi ekivalensi jika dan hanya jika relasi r memenuhi sifat refleksif, simetris, dan transitif.
Source: slideshare.net
Diberikan himpunan c = {2, 4, 5}. Didefinisikan relasi pada himpunan p dengan r={(1,1. Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p. Relasi r dikatakan bersifat antisimetris, apabila untuk setiap (x,y) ∈ r dan (y,x) ∈ r berlaku x = y. Diberikan himpunan c = {2, 4, 5}.
Diberikan himpunan c = {2, 4, 5}.
Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan.
Source: kanaljabar.com
Didefinisikan relasi pada himpunan p dengan r={(1,1. Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Relasi r dikatakan bersifat antisimetris, apabila untuk setiap (x,y) ∈ r dan (y,x) ∈ r berlaku x = y. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}.
Source: slideshare.net
Secara sederhana, relasi dapat didefinisikan sebagai sebuah hubungan, namun hubungan di maksud yaitu hubungan antara daerah asal dan daerah kawan. Relasi r dikatakan bersifat antisimetris, apabila untuk setiap (x,y) ∈ r dan (y,x) ∈ r berlaku x = y. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Didefinisikan relasi pada himpunan p dengan r={(1,1. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}.
Source: youtube.com
Sifat antisimetris misalkan r sebuah relasi pada sebuah himpunan p. Dibmerupakan relasi ekivalensierikan himpunan p = {1,2,3}. Sedangkan fungsi yaitu relasi yang menghubungkan daerah asal.dalam relasi, tidak ada aturan khusus untuk menghubungkan setiap anggota himpunan daerah asal ke. Relasi r dikatakan bersifat antisimetris, apabila untuk setiap (x,y) ∈ r dan (y,x) ∈ r berlaku x = y. Misalkan r sebuah relasi pada sebuah himpunan p.
Situs ini adalah komunitas terbuka bagi pengguna untuk berbagi apa yang mereka cari di internet, semua konten atau gambar di situs web ini hanya untuk penggunaan pribadi, sangat dilarang untuk menggunakan artikel ini untuk tujuan komersial, jika Anda adalah penulisnya dan menemukan gambar ini dibagikan tanpa izin Anda, silakan ajukan laporan DMCA kepada Kami.
Jika Anda menemukan situs ini lengkap, tolong dukung kami dengan membagikan postingan ini ke akun media sosial seperti Facebook, Instagram dan sebagainya atau bisa juga bookmark halaman blog ini dengan judul contoh soal relasi antisimetris dengan menggunakan Ctrl + D untuk perangkat laptop dengan sistem operasi Windows atau Command + D untuk laptop dengan sistem operasi Apple. Jika Anda menggunakan smartphone, Anda juga dapat menggunakan menu laci dari browser yang Anda gunakan. Baik itu sistem operasi Windows, Mac, iOS, atau Android, Anda tetap dapat menandai situs web ini.
